Você já ouviu falar em Padronização e Normalização em Ciência de Dados? Sabe qual a importância desses processos?
Caso prefira esse conteúdo no formato de vídeo-aula, assista ao vídeo abaixo ou acesse o nosso canal do YouTube!
Para receber por e-mail o(s) arquivo(s) utilizados na aula, preencha:
Fala Impressionadores! A Padronização e Normalização em Ciência de Dados são processos muito importantes na hora do tratamento de dados. Assim os algoritmos conseguem fazer suas análises de forma correta sem dar prioridade a uma informação que pode não ser prioritária.
Por esse motivo fazemos esses ajustes, para garantir que a nossa análise vai ficar correta e vai manter a prioridade nas informações corretas.
Isso é muito importante quando temos features com diferentes escalas, o que pode gerar essa priorização de forma errada.
Então, vamos à aula que eu vou te mostrar como fazer o redimensionamento dos dados, padronização, redimensionamento de dados dispersos e muito mais!
Padronização e Normalização em Ciência de Dados
Features com diferentes escalas
“Se uma característica tem uma variância que é de ordem de grandeza maior do que outras, ela pode dominar a função objetivo e tornar o estimador incapaz de aprender com outras características corretamente, como esperado”
Resumindo, o modelo pode colocar mais peso nas variáveis que possuem maior escala e acabar desconsiderando variáveis com menor escala, mas que sejam igualmente ou mais importantes
Ex: comparar salário com número de filhos, essas duas informações na mesma escalas numérica, são dados muito distantes.
Vamos imaginar um salário superior a 3 mil e que o mesmo indivíduo tenha 3 filhos. Não podemos colocar 3mil e 3 na mesma escala porque o valor do salário é muito superior em escala e o código pode desconsiderar a quantidade de filhos que é um dado igualmente relevante ou até mais importante.
O objetivo é colocar todos os nossos recursos em escalas próximas para que o modelo entenda cada um deles como igualmente importantes!
Não estamos mudando o formato dos dados, apenas a escala. Para isso, vamos usar novamente o dataset do titanic
https://www.kaggle.com/competitions/titanic/data
Vamos importar as bibliotecas e visualizar a base:
# Importando o pandas
import pandas as pd
# Importando os dados do titanic
titanic = pd.read_csv('train.csv')
# Visualizando a tabela
titanic.head(3)
# Podemos visualizar as informações estatísticas dessa base
titanic.describe()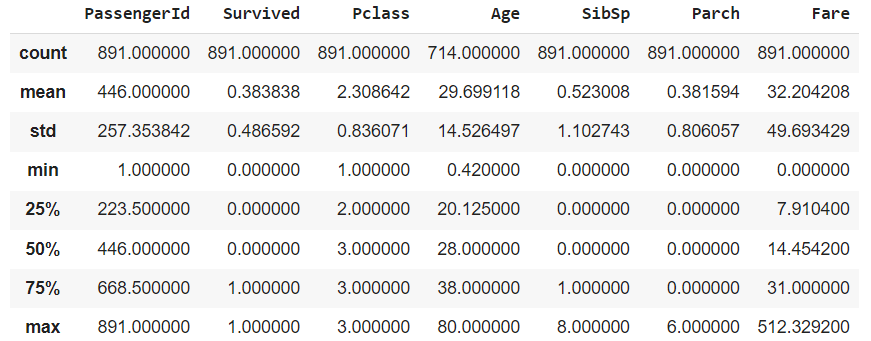
Quando olhamos a tabela fica mais fácil observar a discrepância entre os valores, vemos que as colunas começam e terminam com valores muito distintos.
Vamos começar o tratamento pela coluna Age. Observe que a colunas Pclass e Age estão em escalas muito diferentes e isso pode prejudicar o modelo, principalmente em algoritmos que utilizam distâncias entre os pontos.
Vamos visualizar o boxplot da coluna Age e observar a distribuição dos dados.
# Visualizando o boxplot da coluna Age
titanic.Age.plot.box()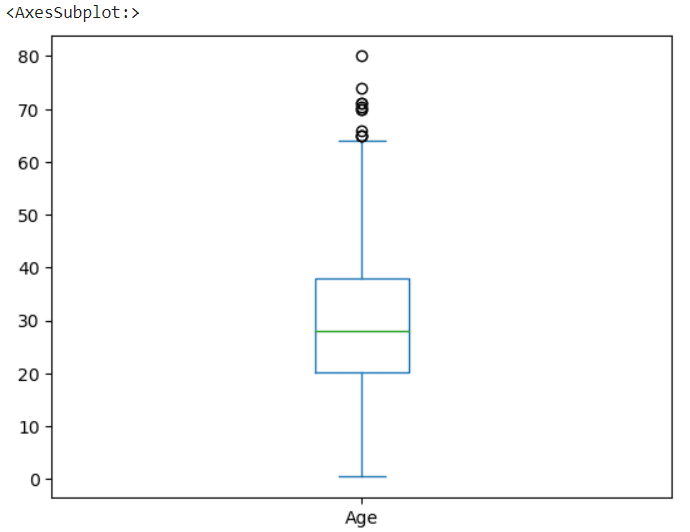
Padronização
É o redimensionamento dos recursos para criar um “padrão” garantindo que os novos dados tenham média zero e desvio padrão igual a 1
A escala padrão de cada valor x será dada por:
z = (x - u) / s, onde:
u: média das amostras
s: desvio padrão das amostrasÉ importante entender a documentação, basicamente o cálculo pega o valor subtrai pela média das amostras e divide pelo desvio padrão.
Fazendo dessa forma é possível garantir que a nova média dos dados vai ser zero e que o desvio padrão vai ser 1. A padronização também facilita a convergência para alguns algoritmos, como o gradiente descendente, ou seja, melhora o modelo.
Vamos começar o processo de Normalização conforme a documentação:
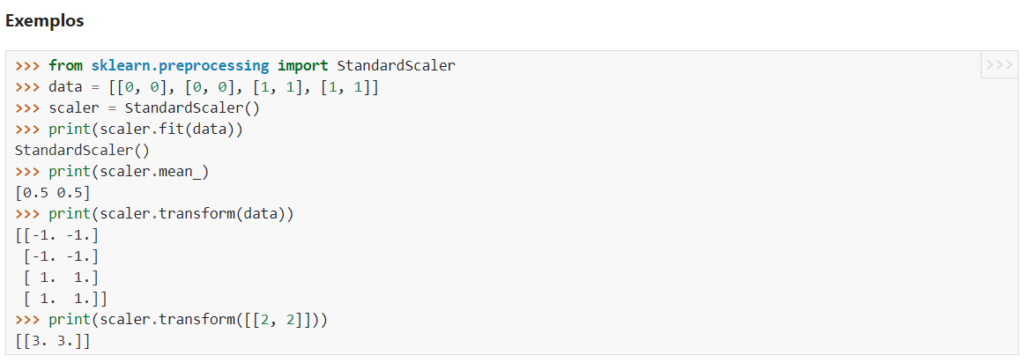
Passo a passo:
# Importando o StandardScaler
from sklearn.preprocessing import StandardScalerNão vamos usar a linha de data com os dados porque já temos os dados do nosso modelo, vamos pular para a próxima linha da documentação -> o scaler.
# Criando nosso scaler
scaler = StandardScaler()Agora iremos fazer o fit com os dados, se você ainda tem dúvidas a respeito de como fazer o fit vou deixar aqui algumas aulas onde explicamos passo a passo como funciona:
REGRESSÃO LINEAR – Algoritmos de aprendizado de máquinas
ÁRVORE DE DECISÃO – Algoritmos de aprendizado de máquinas
# Fazendo o fit com os dados
scaler = scaler.fit(titanic[['Age']])
# Fazendo o transform dos dados e criando a coluna Age_padrao
titanic['Age_padrao'] = scaler.transform(titanic[['Age']])Agora criamos a coluna Age_padrão, vamos visualizar os dados já escalados entre zero e um, observe que existem valores negativos nesta tabela, valores que deveriam ser tratados, porém, para não perder o foco desta aula vamos apenas fazer a normalização, temos uma aula aqui no canal completa sobre limpeza de dados!
# Agora visualizando estatisticamente esses dados
titanic[['Age','Age_padrao']].describe()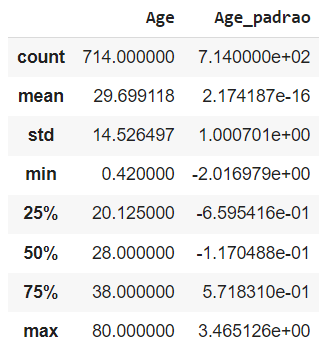
Se compararmos os valores da coluna Age e Age_padrão vemos que os valores da escala já diminuíram muito!
# Podemos inclusive verificar apenas a média
titanic.Age_padrao.mean()
2.1741867565575981e-16
# E o desvio padrão
titanic.Age_padrao.std()
1.0007010165599821Observe que a normalização nada mais é do que colocarmos a média muito próxima a zero e do desvio padrão muito próxima a 1.
Existe outra forma de fazer este tratamento? Sim, podemos fazer o -> Redimensionamento / Scaler
Uma alternativa a padronização é redimensionar os dados entre um valor mínimo e máximo (geralmente entre 0 e 1)
A transformação é dada por:
X_scaled = X_std.(max - min) + min, sendo:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))A explicação detalhada deste cálculo assim como a forma de executar o redimensionamento está disponível na documentação.
Em alguns casos, também vamos ver o redimensionamento com o nome de normalização, isso porque, normalização é um termo genérico, que basicamente diz que estamos adequando os dados a alguma norma…
Normalizer
Existe também o normalizer na documentação, mas vamos falar do normalizer mais para a frente, é diferente do que estamos mostrando agora!
Em geral, vamos obter desvios padrões menores (dados mais concentrados próximo à média) e é muito útil quando queremos manter os valores zeros do dataset.
Vamos começar o redimensionamento seguindo as instruções da biblioteca
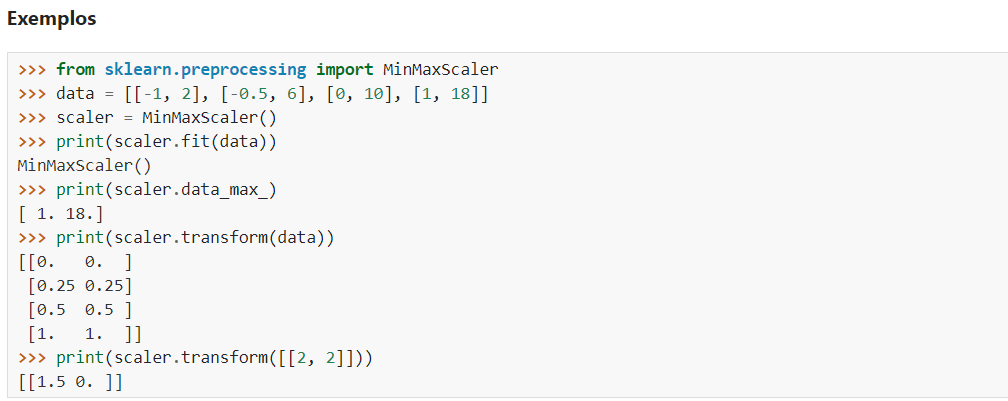
# Importando o MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
# Criando o scaler
scaler = MinMaxScaler()
# Fazendo o fit com os dados
scaler = scaler.fit(titanic[['Age']])
# Fazendo a transformação e criando a coluna Age_minmax
titanic['Age_minmax'] = scaler.transform(titanic[['Age']])
# Visualizando novamente os dados
titanic[['Age','Age_padrao','Age_minmax']].describe()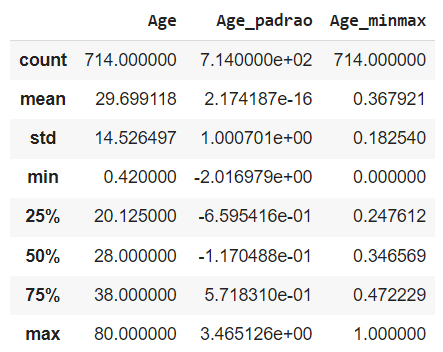
Observe que, do mesmo modo conseguimos um desvio padrão mínimo 0 e máximo 1.
Mas, e se estivermos trabalhando com dados dispersos? Se os dados estiverem muito espalhados ou negativos?
Redimensionando dados dispersos
O MaxAbsScaler funciona de uma maneira semelhante, porém dividindo todos os dados pelo máximo absoluto daquela coluna
Isso faz com que o range seja de -1 a 1 caso existam valores negativos, funciona muito bem para trabalhar com dados esparsos (dispersos / espalhados)
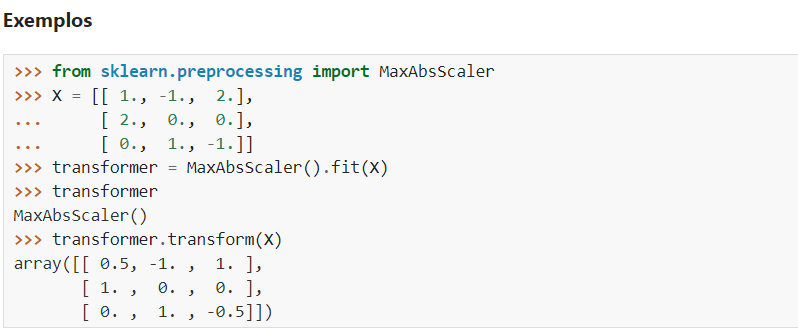
Passo a passo seguindo a documentação:
# Importando o MaxAbsScaler
from sklearn.preprocessing import MaxAbsScaler
# Criando o scaler
scaler = MaxAbsScaler()
# Fazendo o fit com os dados
scaler = scaler.fit(titanic[['Age']])
# Fazendo a transformação e criando Age_maxabs
titanic['Age_maxabs'] = scaler.transform(titanic[['Age']])
# Visualizando novamente os dados
titanic[['Age','Age_padrao','Age_minmax','Age_maxabs']].describe()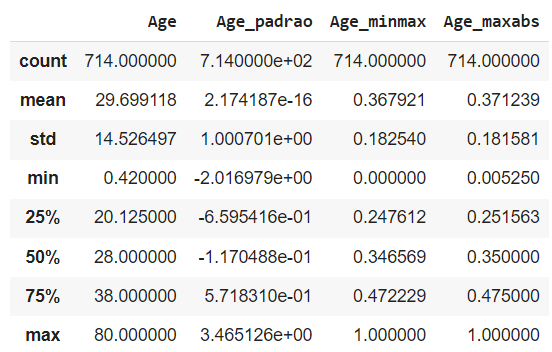
Redimensionando dados com outliers
Se os dados tiverem muitos outliers, utilizar os métodos mostrados anteriormente pode não funcionar tão bem, isso porque os outliers vão ter dados iguais a 1 e os demais dados vão ficar muito próximos de zero. Como alternativa podemos utilizar o RobustScaler
Esta biblioteca vai usar o interquartil como base do redimensionamento
Interquartil: Q3 – Q1

Passo a passo seguindo a documentação:
# Importando o RobustScaler
from sklearn.preprocessing import RobustScaler
# Criando o scaler
scaler = RobustScaler()
# Fazendo o fit com os dados
scaler = scaler.fit(titanic[['Age']])
# Fazendo a transformação e criando Age_robust
titanic['Age_robust'] = scaler.transform(titanic[['Age']])
# Selecionando as colunas que queremos analisar
colunas = titanic.columns[titanic.columns.str.contains('Age')]
# Visualizando novamente os dados
titanic[colunas].describe()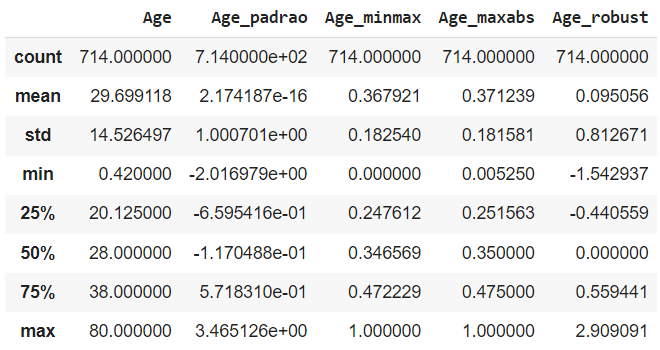
Perceba que o Age_robust tenta desconsiderar os outliers e por este motivo seu vamos mínimo e máximo passam a permear entre 0,81 e 2,9
Visualizando graficamente
# Importando o seaborn
import seaborn as sns
# Visualizando graficamente
import matplotlib.pyplot as plt
fig, ax = plt.subplots(ncols=3,figsize=(15,6))
sns.kdeplot(titanic.Age,ax=ax[0])
sns.kdeplot(titanic.Age_padrao,ax=ax[1],label='padrão')
sns.kdeplot(titanic.Age_robust,ax=ax[1],label='robust')
sns.kdeplot(titanic.Age_minmax,ax=ax[2],label='minmax')
sns.kdeplot(titanic.Age_maxabs,ax=ax[2],label='maxabs')
ax[1].legend()
ax[2].legend()
plt.show()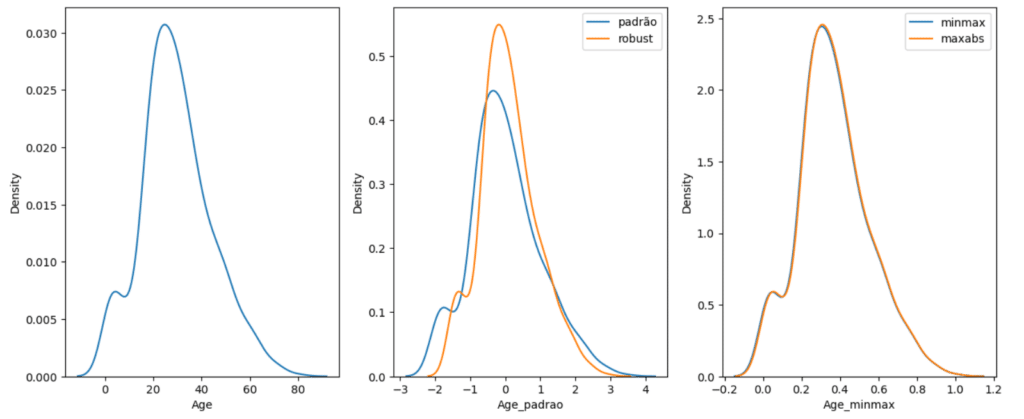
Visualizando os gráficos fica mais fácil perceber que todas as transformações que fizemos até agora possuem o mesmo formato
Podemos fazer o cálculo do mínimo e máximo para cada um desses valores e entender o que cada uma dessas transformações fazem:
# Visualizando novamente a descrição estatística
titanic[colunas].describe()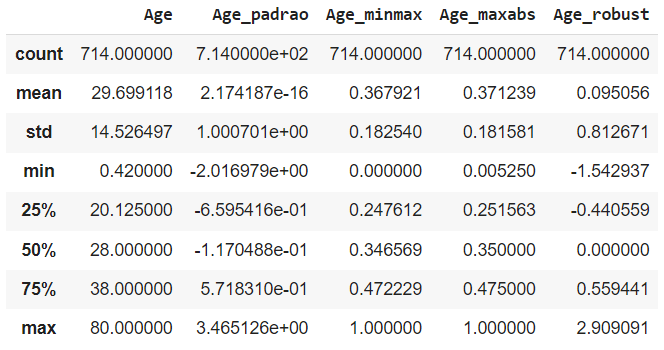
# Visualizando a média da coluna
media = titanic.Age.mean()
media
29.69911764705882
# O desvio padrão
desvio = titanic.Age.std()
desvio
14.526497332334044
# O mínimo
minimo = titanic.Age.min()
minimo
0.42
# E o máximo
maximo = titanic.Age.max()
maximo
80.0Lembra quando mostrei que o cálculo consiste em pegar o valor e fazer a média dele dividido pelo desvio padrão? Vamos agora fazer os cálculos para cara transformação feita?
Calculando para o StandardScaler
# O mínimo
(minimo-media)/desvio
-2.0155662426542023
# O máximo
(maximo-media)/desvio
3.462698625977656Observe que o valor mínimo e máximo encontrados é muito próximo ao encontrado na descrição estatística.
Para o MinMaxScaler, o mínimo vai ser 0 e o máximo vai ser 1. Agora verificando para o MaxAbsScaler:
# O mínimo
minimo/maximo
0.0052499999999999995
# O máximo
maximo/maximo
1.0E para o RobustScaler?
Para o RobustScaler nós não utilizamos a média nem o desvio padrão, porque não queremos que ele seja afetado por outliers. Então vamos utilizar a mediana e os quartis.
# Calculando a mediana da coluna Age
mediana = titanic.Age.median()
mediana
28.0
# Verificando o primeiro quartil
q1 = titanic.Age.describe()['25%']
q1
20.125
# O terceiro quartil
q3 = titanic.Age.describe()['75%']
q3
38.0
# E o interquartil
interquartil = q3-q1
# Agora calculando para o mínimo
(minimo - mediana)/interquartil
-1.542937062937063
# E para o máximo
(maximo - mediana)/interquartil
2.909090909090909Antes de fechar esta aula, vou explicar o Normalizer.
Normalizer:
O normalizer basicamente vai funcionar nas linhas, não nas colunas, tudo que vimos até agora estava considerando as colunas
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.Normalizer.html
“Cada linha da matriz de dados com pelo menos um componente diferente de zero é redimensionada independentemente de outras amostras para que sua norma seja igual a um“
Segundo a própria documentação, é mais usado em classificação de texto ou agrupamento!

Passo a passo seguindo a documentação:
# Importando o Normalizer
from sklearn.preprocessing import Normalizer
# Sendo X dado pelos valores abaixo
X = [[4, 1, 2, 2],
[1, 3, 9, 3],
[5, 7, 5, 1]]
# Vamos criar o nosso "normalizador"
transformer = Normalizer(norm='l1')
# E fazer o fit com os dados
transformer = transformer.fit(X)
# Fazendo o transform e salvando em um array
array_norm = transformer.transform(X)
array_norm
# Elevando esse array ao quadrado
array_norm**2
# Elevando esse array ao quadrado e somando as linhas
(array_norm**2).sum(axis=1)
array([1., 1., 1.])Neste caso estamos usando como parâmetro o L1, então a soma dos valores da linha será igual a 1, se o parâmetro usado for o L2 (documentação) então o cálculo muda, neste caso o quadrado da soma das linhas será igual a 1. Em todo caso vamos conseguir normalizar os valores.
Nesta aula apresentei a vocês os diferentes modos de tratar dados em escala.
Trouxe cada conceito e bibliotecas, assim como um passo a passo de como fazer os tratamentos.
Nas próximas aulas vamos utilizar esses conceitos, na prática, e mostrar como esses tratamentos conseguem melhorar o nosso modelo!
Eu espero que tenham gostado! Até mais! Abraço,
Para acessar outras publicações de Ciência de Dados, clique aqui!
Expert em conteúdos da Hashtag Treinamentos. Auxilia na criação de conteúdos de variados temas voltados para aqueles que acompanham nossos canais.