Dando sequência ao nosso aprendizado sobre algoritmos de aprendizagem de máquinas, hoje vamos fazer previsões com regressão linear.
Caso prefira esse conteúdo no formato de vídeo-aula, assista ao vídeo abaixo ou acesse o nosso canal do YouTube!
Para receber por e-mail o(s) arquivo(s) utilizados na aula, preencha:
Na última aula sobre Algoritmos de Aprendizado de Máquinas falamos sobre árvore de decisão usada para classificação, estávamos falando sobre classificar valores como 0 ou 1, como fraude ou não-fraude ou classificar uma fruta como banana ou maçã.
Neste caso temos valores nominais e queremos descobrir qual é o valor de cada um dos registros, buscando prever essas classes.
Se você não sabe o que é arvore de decisão ou quiser saber mais, vou deixar o link aqui para você, árvore de decisão.
Agora nós vamos falar sobre um problema um pouco diferente, vamos falar sobre Previsões com Regressão Linear.
Ao invés de ter uma classe que pode ser fraude ou não-fraude, vamos ter valores contínuos que vamos usar para prever qual seria a venda que faríamos ao aplicar um determinado desconto, por exemplo.
Quando eu dou um desconto de 1 real eu vendo determinado valor, quando eu dou um desconto maior o meu valor de vendas também muda, podemos perceber que existe uma relação entre essas duas variáveis.
Nosso objetivo é procurar qual é essa relação para podermos prever novos descontos utilizando a progressão linear.
Considerando os 5 pontos no gráfico de dados que nós já temos, qual seria nossa melhor estimativa?
Se temos um conjunto de pontos como na imagem abaixo, podemos traçar qualquer reta que passe por esses pontos.
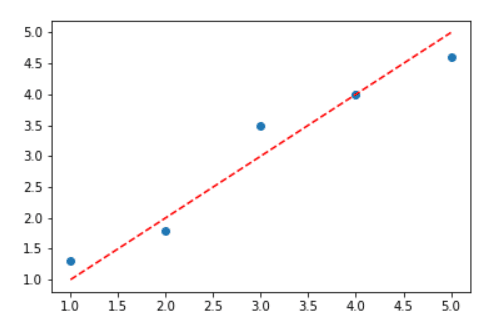
Nesse caso, vamos traçar uma reta y = x.
Infinitas retas podem ser traçadas, mas qual seria a melhor reta que passa por esses pontos?
Observe que na imagem abaixo uma reta está muito afastada das demais, ela não é a melhor reta para fazermos as Previsões com Regressão Linear devido a esta distância.
Isso significa que a melhor reta é a que possui a menor distância em relação aos cinco pontos.
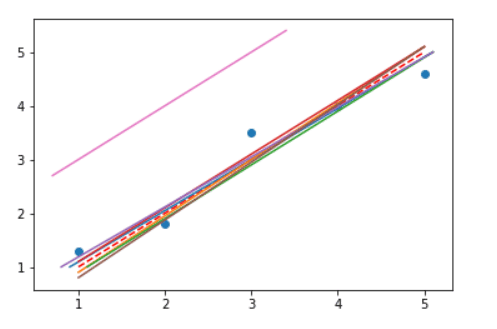
Para definir esse conceito podemos, por exemplo, verificar a distância de cada ponto em relação à reta vermelha, calcular essas distâncias e escolher baseado no menor resultado.
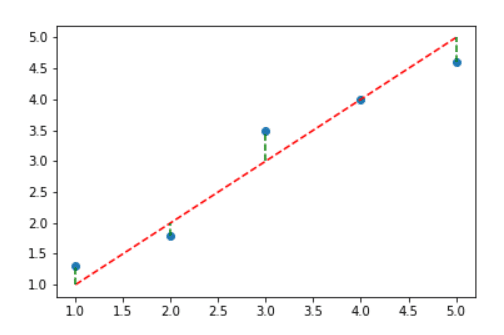
Ou seja, sabendo a distância entre cada ponto e calculando essas distâncias podemos saber qual a melhor reta.
A regressão linear vai traçar essa reta para minimizar a soma dos erros ao quadrado, segundo a própria documentação que vou deixar no link aqui abaixo:
https://scikit-learn.org/stable/modules/linear_model.html#ordinary-least-squares
Veja que as Previsões com Regressão Linear consegue sozinha gerar a melhor reta para estes pontos!
Vamos começar importando os pontos dessa base para fazermos passo a passo esse mesmo algoritmo de regressão do exemplo acima.
Após importar os pontos vamos fazer um gráfico com eles.
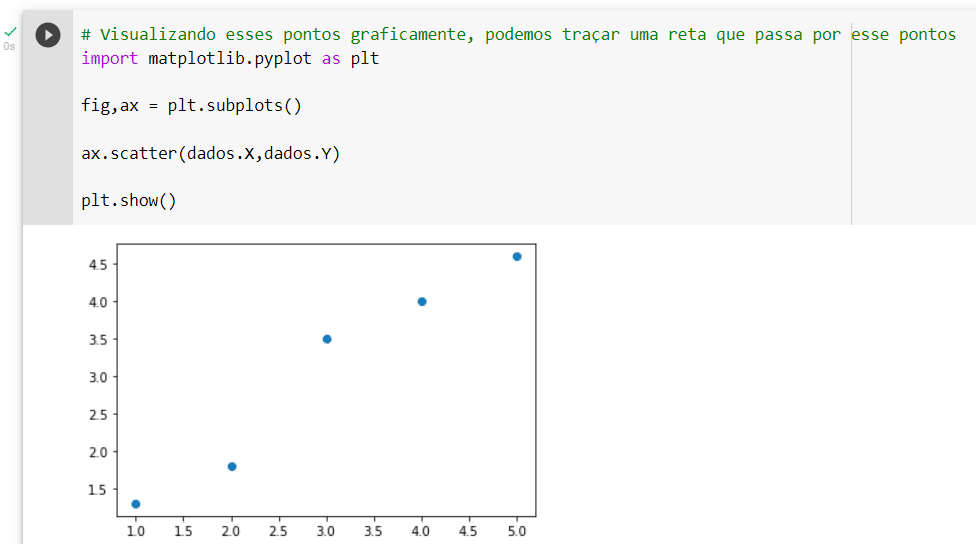
Ok, você lembra que na primeira reta eu falei que nós estávamos traçando uma reta y = x.
Podemos traçar essa reta na nossa base. Podemos adicionar uma coluna que vai ser o y da reta e essa coluna vai receber os nossos valores de x já que a minha reta é y = x.

Neste caso, que já temos os valores dos pontos, nós podemos apenas acrescentar a reta com os valores de x e a reta que acabamos de criar.
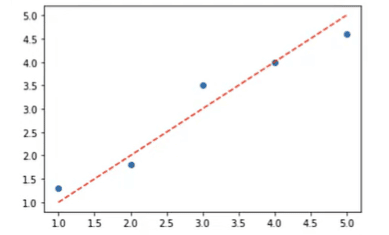
Se quisermos traçar os pontos em cima da reta também podemos acrescentá-los.

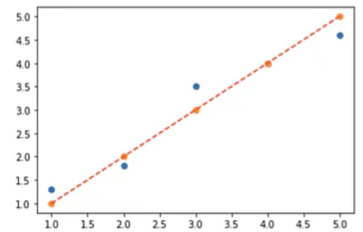
Certo, mas essa é a melhor previsão que podemos fazer?
Com certeza não, eu vou mostrar para você como fazer a regressão linear e como a gente calcula a distância ao quadrado entre o ponto e a reta.
Isso é bom para que você possa comparar e ver que a reta da regressão linear tem uma distância menor.
Vamos utilizar a regressão linear para traçar a melhor reta que passa por esses pontos.
Clique no link para começarmos a criar a nossa regressão:
Tudo que vamos utilizar para fazer a regressão existe nesta documentação.

Nós apenas vamos copiar da própria documentação e colocar no nosso código.
Vamos completar # Importando a regressão linear com a segunda linha da documentação.

A terceira, quarta e quinta linha definem x e y, como nós já temos esta definição vamos passar para a próxima linha que serve para criar uma regressão.
Vamos utilizar a sexta linha da documentação para criar a regressão, apenas teremos que fazer um pequeno ajuste para identificar x e y corretamente.
Além disso, o código espera receber o Two-dimensional array (2D array).
Mas como sabemos disso?
Sabemos por que se executarmos o código ele vai dar um erro justamente pedindo para colocar o 2D array.

Para fazer isso nós temos que acrescentar um reshape no nosso código, vamos usar o que foi indicado na correção.
Porém, existe um detalhe, para fazer isso nós iremos pegar apenas os valores de x, se tentarmos fazer isso no Dados.x que é uma série do Pandas vai resultar em erro porque não tem a propriedade reshape.
Se você não lembra o que é séries ou não conhece o Pandas vou deixar um link de introdução ao pandas para te ajudar.
O que nós queremos é apenas os valores de x, para pegar apenas os valores de x é só utilizar o values.

Agora conseguimos criar o nosso regressor, sendo nosso modelo utilizando a regressão linear.
Esse regressor vai ter duas propriedades que serão muito importantes.
A primeira delas é o coeficiente angular, lembra quando falamos de retas, que elas possuem um coeficiente angular?
Neste temos o coeficiente angular e o linear, adicionando os dois nós conseguimos traçar uma reta como nas equações de primeiro grau, equações da reta.

Agora o que temos que fazer é copiar o gráfico que já tínhamos feito, colar em uma nova linha de código e traçar a reta gerada pelo novo regressor.
O que vai ser o meu x?
O meu x vai ser o dados.x.values.
Já para o nosso y nós vamos usar a equação da reta que diz que y = ax+b.
Segue abaixo o valor de A e B:
A = reg.coef_[o]
B= reg.intercept_
Neste caso que temos x e y eu posso fazer um plot considerando o x e o y:
Ax.plot(x,y)
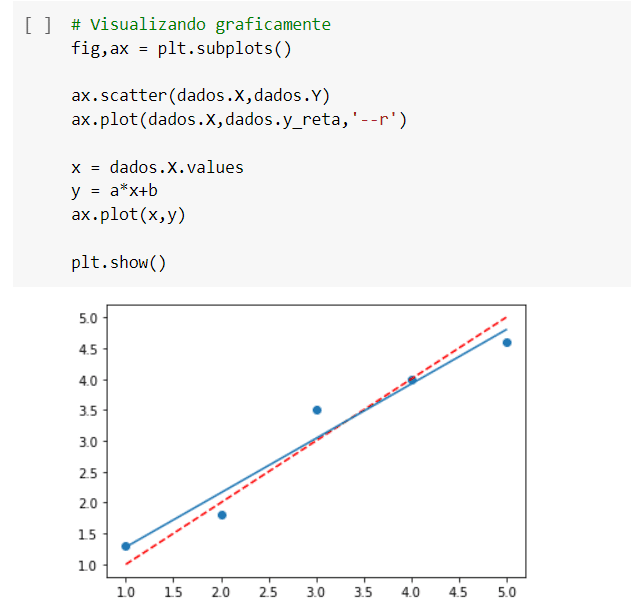
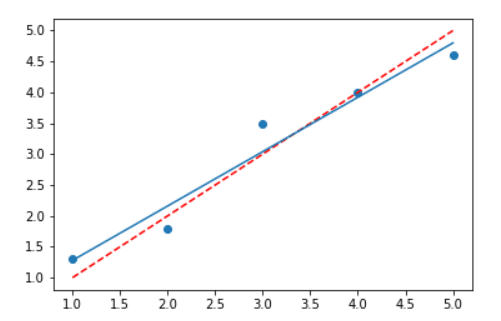
Agora nós temos a reta que melhor se ajusta aos nossos pontos.
Como posso ter certeza de que esta é a melhor reta?
Como saber e como provar isso?
Que a reta recém-criada em azul é melhor que a anterior tracejada em vermelho na imagem acima?
Vamos fazer isso começando pela previsão, qual é a previsão que esse regressor que acabamos de criar gerou.
Vamos usar o reg.predict e passar os nossos dados, da mesma forma que usamos o reshape anteriormente, aqui precisaremos usar o mesmo reshape.
Após salvar os dados vamos verificar o erro como na imagem abaixo.
O erro vai ser a diferença entre um valor e outro elevado ao quadrado, vamos fazer exatamente isso.

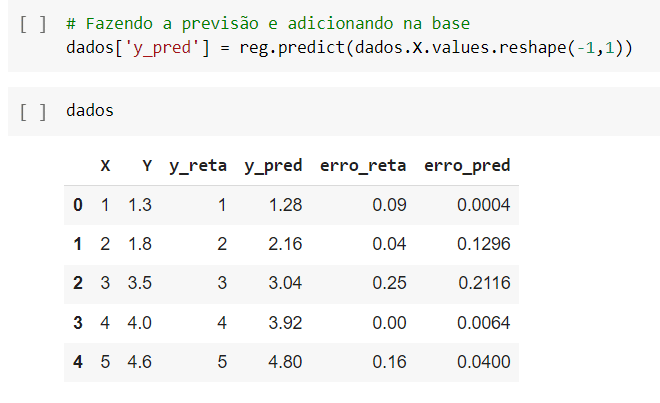
Agora que temos os resultados dos erros das duas retas, podemos calcular e ver qual das duas se ajusta melhor aos pontos.
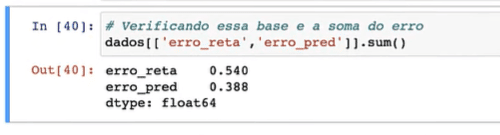
Utilizando apenas os resultados do erro_reta e erro_pred vemos que o erro_pred está menor, portanto, mais próximo dos pontos da reta.
Então para saber qual das previsões teve o menor desvio vamos sempre ter que calcular a diferença entre os erros?
Não, porque o próprio scikit-learn já oferece métricas de cálculos de erro, tanto métricas de classificação quanto métricas de regressão.
Podemos importar as métricas do scikit-learn.
https://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics
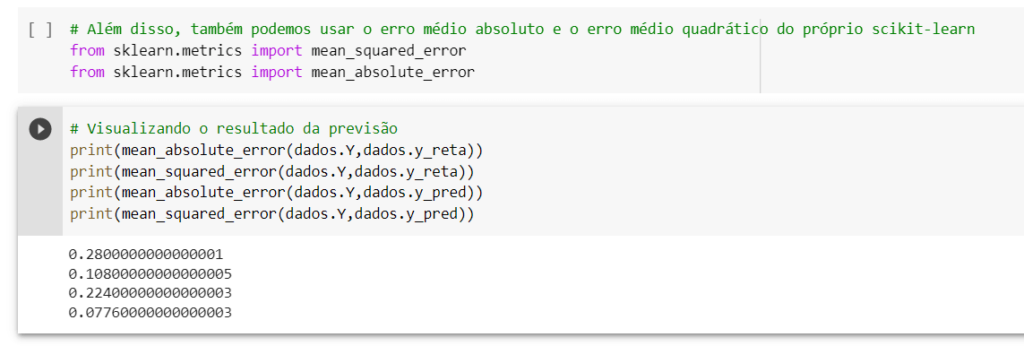
Aqui podemos ver novamente que o resultado de y_pred está com uma diferença menor que o y_reta.
Obs. Os resultados ficaram diferentes da primeira regressão porque no primeiro cálculo que fizemos somamos os valores e neste cálculo estamos utilizando a média.
Não vamos nos aprofundar muito sobre os erros porque já temos uma aula completa sobre avaliação de erros em modelos de regressão, se você quer saber mais clique no link!
Vamos utilizar o dataset de casas da Califórnia.
https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html
Vamos importar uma base de dados reais do link acima.
Utilizaremos este dataset:
Vamos importar uma base de dados reais do link acima.
Utilizaremos este dataset:
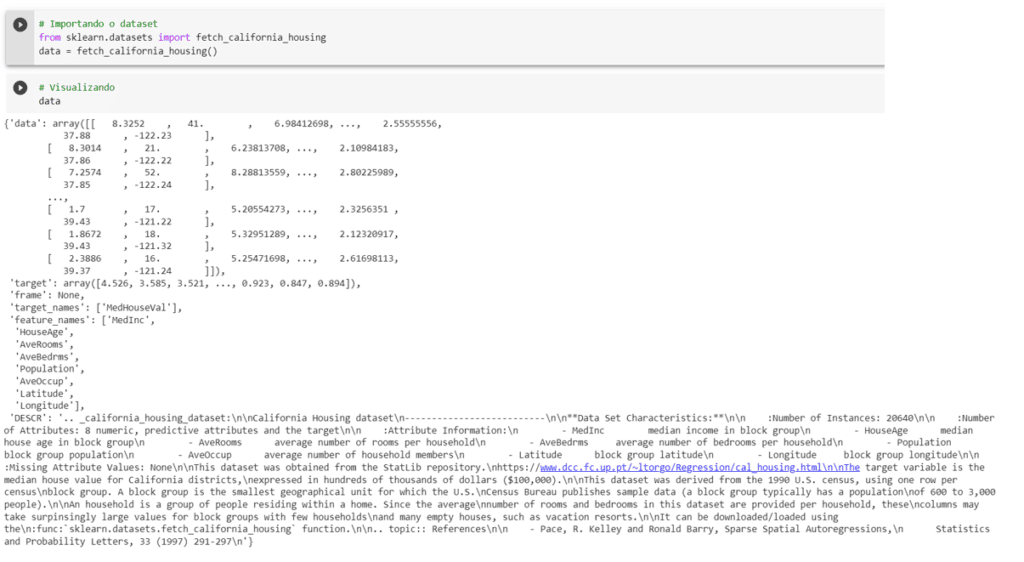
Neste dataset temos as colunas, os targets o nome de cada uma das colunas etc.
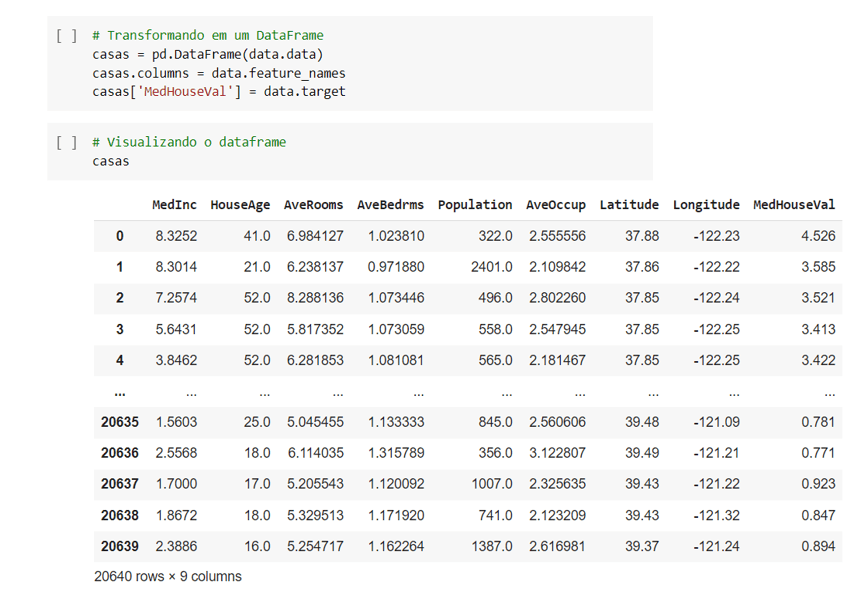
Agora com as informações da base de dados podemos transformar isso em um DataFrame.
Nós podemos utilizar data ou qualquer nome que você queira criar → colocar o sinal de igual (=) → e a base de dados importada.
Começamos passando as informações de (data.data).
Se quisermos visualizar é só digitar casas na próxima linha de código.
Para visualizar o nome de cada coluna podemos utilizar o ‘feature_names’.
Fazendo isso vamos visualizar tudo certinho com o nome de cada coluna.
Para fechar vamos criar uma coluna com os targets, observe na foto abaixo a organização das linhas, todas as informações foram importadas no nosso dataset.
Só pegamos o Dataset e transformamos em um DataFrame do Pandas.
Vamos utilizar agora a regressão linear simples.
Para começar vamos pegar uma única coluna, porque na regressão linear simples nós relacionamos uma coluna com o nosso target.
Já na regressão linear múltipla nós vamos relacionar mais de uma coluna.
Observe abaixo a organização das linhas de código.
Previsões com Regressão Linear Simples.
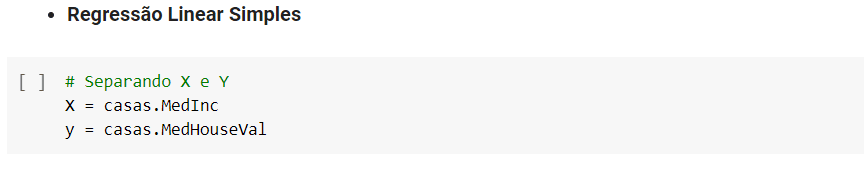
Após definir o x e y vamos separar nossa base em treino e teste para criarmos o modelo.
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
Vamos importar as informações do link acima, o train_test_split, os dados de treino e os dados de testes.
Por que nós precisamos dos dados de treino e de teste?
Poque nós vamos primeiro treinar o modelo com os dados de treino e depois usar os dados de teste para avaliar o nosso modelo.
Como já temos o x e o y podemos agora fazer a regressão linear, é só copiar o código que já fizemos da linha de código #criando o regressor e colar na próxima linha de código, mudando os dados.x e dados.y pelos dados de treino.
Feito isso vamos avaliar o erro da mesma maneira que fizemos no início da aula.

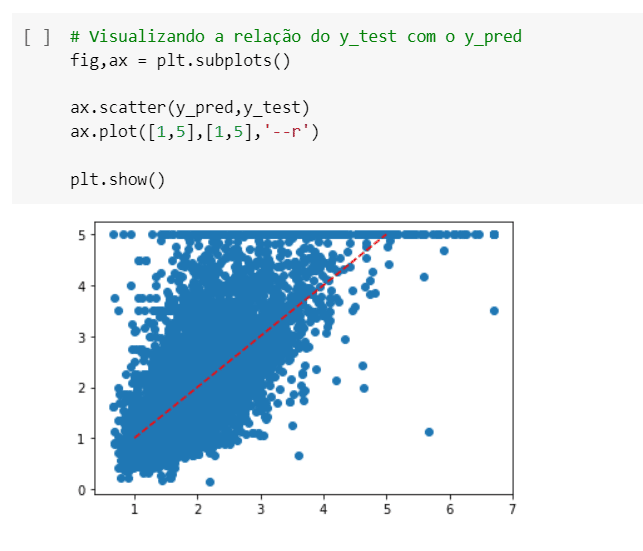
Conseguimos gerar os resultados, também podemos gerar esse resultado de uma forma mais visual, com gráficos.
Podemos fazer um gráfico de dispersão.
Vamos aqui criar uma reta que seja x=y para podermos ver qual o valor que a gente tinha e qual valor a gente previu.
Assim conseguimos verificar o quão bem estamos fazendo as nossas previsões visualmente além de acompanhar os indicadores.
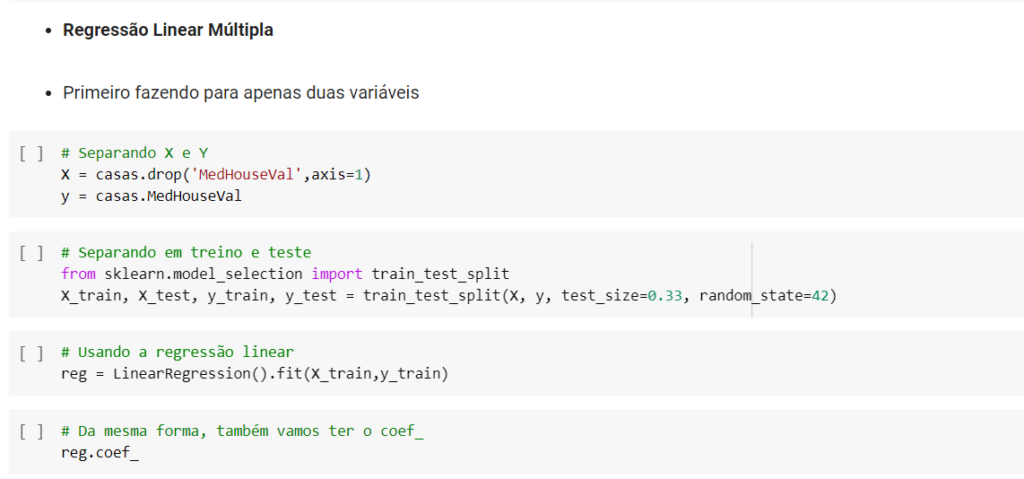
Nós usamos a regressão linear simples como exemplo, mas também podemos usar a regressão linear múltipla.
Podemos escolher duas colunas que sejam boas para prever o comportamento de preço.
Neste exemplo vou usar a coluna com a média de banheiros.
Vamos utilizar a mesma lógica usada na regressão linear com algumas, sutis diferenças.
Quando o gráfico for gerado, nós podemos comparar os resultados e ver se a projeção melhorou ou piorou em relação à última regressão linear simples que fizemos.
Previsões com Regressão Linear Múltiplas.

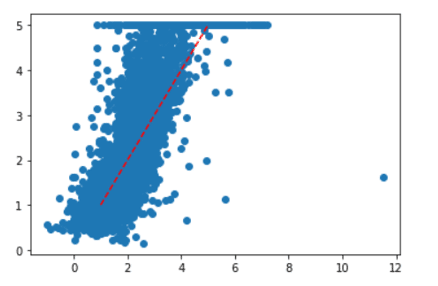
Podemos também voltar e utilizar todas as colunas para a projeção, depois testar se o erro diminui, se o nosso resultado melhora.
Obs. Ao utilizar todas as colunas não esqueçam de retirar a coluna que estamos querendo prever.
Observe que agora a dispersão do gráfico melhorou.
Então o modelo com todas as colunas gerou uma previsão muito melhor!
Ao invés de ter um único coeficiente angular, nós vamos ter o valor que vai multiplicar cada uma das colunas.
Assim testando vários modelos podemos definir qual deles vai nos dar o resultado mais assertivo.
Nesta aula vimos em um passo a passo como utilizar o modelo de regressão para resolver problemas de ciências de dados e prever informações.
Vimos como usar dataset e transformá-los em DataFrame para que seja possível trabalhar de forma eficiente.
Eu fico por aqui! Espero que tenham gostado! Até breve,
Para acessar outras publicações de Ciência de Dados, clique aqui!
Expert em conteúdos da Hashtag Treinamentos. Auxilia na criação de conteúdos de variados temas voltados para aqueles que acompanham nossos canais.