O que é o Perceptron? Você já conhece a estrutura de redes neurais? Nesta aula vamos dar continuidade a explicação com exemplos práticos!
Caso prefira esse conteúdo no formato de vídeo-aula, assista ao vídeo abaixo ou acesse o nosso canal do YouTube!
Para receber por e-mail o(s) arquivo(s) utilizados na aula, preencha:
Fala Impressionadores! Você já ouviu falar no Perceptron? Sabe o que é ou como ele funciona?
Nessa aula eu vou te mostrar o que é o Perceptron, como ele funciona e um pouco da história dele.
O Perceptron é a estrutura base de redes neurais e Deep learning, clique no link da última aula! Vale a pena conferir. Você vai ver em vários casos o uso do Perceptron para classificação de dados.
Vamos utilizar o Dataset Íris como base para fazer o nosso exemplo, esse é um dataset já conhecido, mas se não conhece, não tem problema, você vai conseguir acompanhar a nossa análise de dados!
Vou te mostrar 2 exemplos, um onde temos dados linearmente separáveis e outro onde temos dados não linearmente separáveis.
Além disso, ainda quero te mostrar o problema do OR e XOR no Perceptron que “congelou” ele por muito tempo.
O Perceptron
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
O Perceptron é usado para resolver diversos problemas como:
Este é um modelo linear para classificação binária. Só é possível fazer a separação se os dados forem linearmente separáveis.
O seu aprendizado é feito através do cálculo dos pesos e vieses e o seu funcionamento é baseado no funcionamento do neurônio humano:
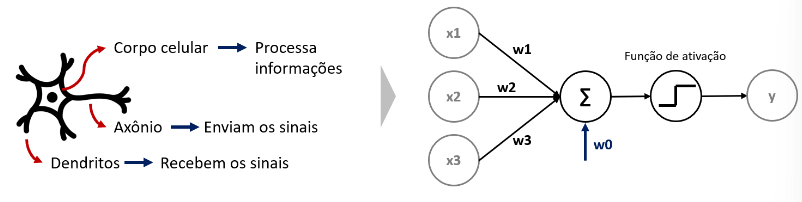
A ideia do Perceptron é justamente copiar o funcionamento do nosso neurônio.
Foi proposto em 1943 por McCulloch e Pitts e implementado pela primeira vez em 1958 por Frank Rosenblatt segundo o The New York Times:
O perceptron é “o embrião de um computador eletrônico que [a Marinha] espera que seja capaz de andar, falar, ver, escrever, reproduzir-se e ter consciência de sua existência”
Devido a sua limitação de prever padrões simples como o OU exclusivo (XOR), ficou um tempo “congelado”, mas foi retomado fortemente com o avanço do Deep Learning
[ ]
# Importando as bibliotecas
import pandas as pd
import matplotlib.pyplot as plt
import numpy as npVamos usar o dataset iris:
# Importando o dataset iris
from sklearn.datasets import load_iris
# Determinando o X e y
X_iris,y_iris = load_iris(return_X_y=True, as_frame=True)
# Visualizando
X_iris.head(3)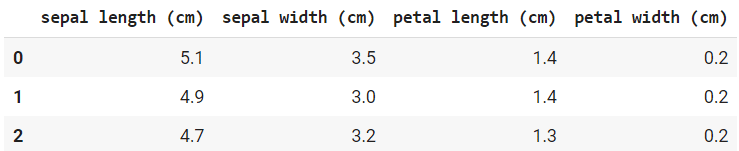
# Selecionando apenas as colunas de pétala e o target 0 e 1
X = X_iris.loc[y_iris.isin([0,1]),['petal length (cm)','petal width (cm)']]
y = y_iris.loc[y_iris.isin([0,1])]
# Verificando o valor de y
y.value_counts()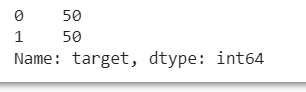
# Observando graficamente os dados
fig, ax = plt.subplots()
ax.scatter(X.iloc[:,0],X.iloc[:,1],c=y)
ax.set(xlim=(0.9,5.2),xticks=[1,2,3,4,5],
ylim=(0,2),yticks=[0,1,2])
plt.show()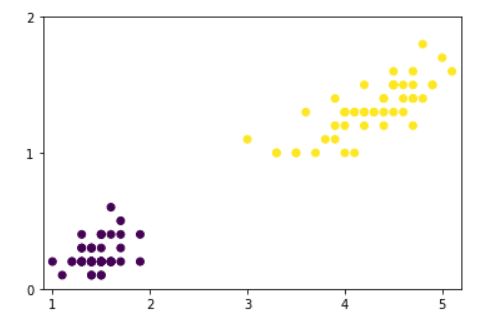
O que acabamos de fazer foi separar os dados em 0 e 1. Observe que o gráfico mostra os pontos linearmente separáveis, porque aqui somos capazes de traçar uma linha entre esses dados e classificar tudo que estiver acima da linha e tudo que estiver abaixo dela.
Vamos entender observando a figura abaixo:
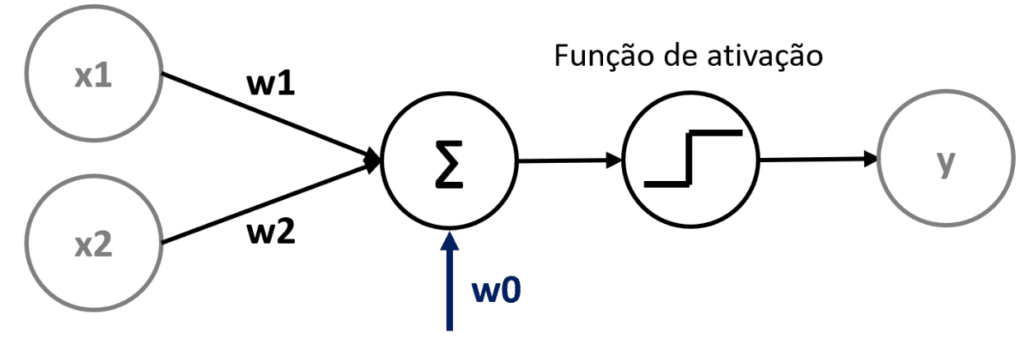
Neste exemplo temos dois valores que estão sendo passados, esses valores estão recebendo um peso, em seguida recebem um valor fixo e a partir daí seguem para a função de ativação, o resultado será nosso y.
É importante lembrar que por mais que temos no gráfico a reta horizontal correspondendo ao x e a reta vertical correspondendo ao y, neste caso consideramos a reta horizontal como X1 e vertical como X2.
Estou apenas reforçando essas classificações para não haver confusão com o y, que é o que estamos querendo prever.
Agora, vamos importar o Perceptron e fazer a classificação conforme a documentação:
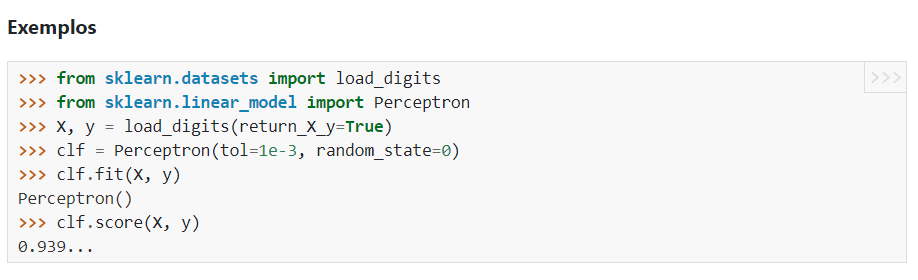
Podemos utilizar o Perceptron para separar esses dados
# Separando em treino e teste
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Importando o Perceptron
from sklearn.linear_model import Perceptron
# Criando o classificador
clf = Perceptron(tol=1e-3, random_state=0,eta0=0.1)
# Fazendo o fit com os dados
clf = clf.fit(X_train,y_train)
# Fazendo a previsão
y_pred = clf.predict(X_test)Podemos utilizar a matriz de confusão para avaliar esse modelo
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html
# Importando a matriz de confusão
from sklearn.metrics import confusion_matrix
# Avaliando o modelo
confusion_matrix(y_test,y_pred)
Entendendo o que o Perceptron fez.
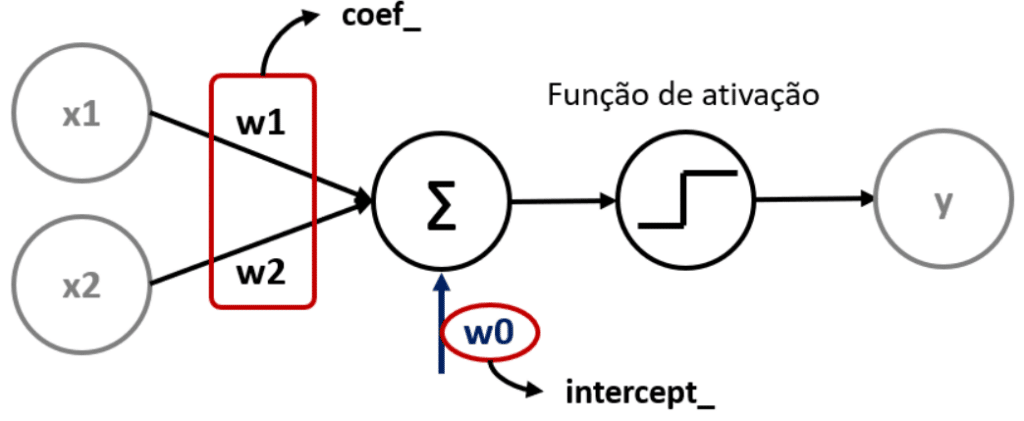
X_train.head(3)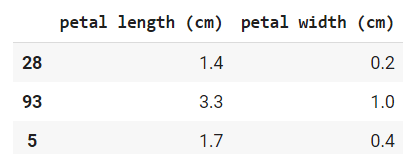
Esses são os valores do meu input, ou seja, os dados de entrada.
Neste caso estamos começando com os valores de 1,4 e 0,2 e vamos começar com o peso valendo 0 e 0 também.
Após definir o valor e peso vamos multiplicar o valor pelo peso, somar esses valores e, após isso, somar com o intercept_
Na parte de baixo da função de ativação a classe é 0 e na parte de cima corresponde a 1, neste caso nosso y é zero e a decisão está correta.
Após calcular a primeira linha e ele vai passar para a segunda e assim sucessivamente.
y_train[:3]
E esses são os dados do output, dados de saída do nosso modelo.
# Verificando o coef_
clf.coef_
array([[0.08, 0.08]])
# E o intercept
clf.intercept_
array([-0.2])
# Podemos escrever w1, w2 e w0 como
w1 = round(clf.coef_[0][0],2)
w2 = round(clf.coef_[0][1],2)
w0 = clf.intercept_[0]
print(w1,w2,w0)
0.08 0.08 -0.2O resultado será como mostrado na figura:
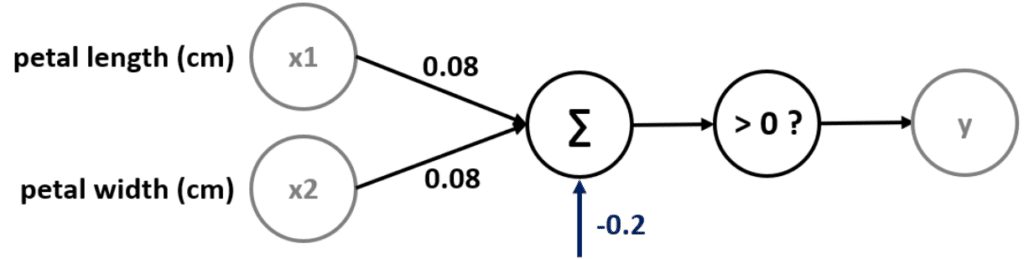
Após definir o valor e peso vamos multiplicar o valor pelo peso (0,08), somar esses valores e, após isso, somar com o intercept (-0,2).
Classificação
Se o resultado for maior que zero a classificação será 1, se for menor ou igual a zero a classificação será zero.
Podemos visualizar graficamente:
# Adicionando essa reta no gráfico
fig, ax = plt.subplots()
ax.scatter(X_train.iloc[:,0],X_train.iloc[:,1],c=y_train)
ax.plot(X_train.iloc[:,0],(-w1*X_train.iloc[:,0]-w0)/w2)
ax.scatter(X_test.iloc[:,0],X_test.iloc[:,1],c=y_test)
ax.set(xlim=(0.9,5.2),xticks=[1,2,3,4,5],
ylim=(0,2),yticks=[0,1,2])
plt.show()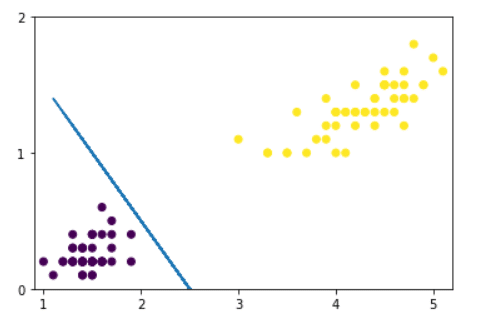
O que acontece se tentarmos separar as classes 1 e 2?
# Agora considerando as classes 1 e 2
X = X_iris.loc[y_iris.isin([1,2]),['petal length (cm)','petal width (cm)']]
y = y_iris.loc[y_iris.isin([1,2])]
# Observando graficamente os dados
fig, ax = plt.subplots()
ax.scatter(X.iloc[:,0],X.iloc[:,1],c=y)
ax.set(xlim=(2.9,7),xticks=[3,4,5,6,7],
ylim=(0.9,3),yticks=[1,2,3])
plt.show()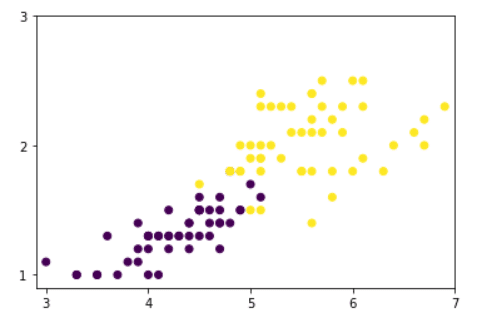
# Separando em treino e teste
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Criando um classificador
clf = Perceptron(tol=1e-3, random_state=0,eta0=0.1)
# Fazendo o fit com os dados
clf = clf.fit(X_train,y_train)
# Fazendo a previsão
y_pred = clf.predict(X_test)
# Avaliando o modelo
confusion_matrix(y_pred,y_test)
array([[19, 2],
[0, 12], dtype=int64)# Podemos escrever w1, w2 e w0 como
w1 = round(clf.coef_[0][0],2)
w2 = round(clf.coef_[0][1],2)
w0 = clf.intercept_[0]
print(w1,w2,w0)
-0.24 3.07 -3.800000000000002
# Adicionando essa reta no gráfico
fig, ax = plt.subplots()
ax.scatter(X_train.iloc[:,0],X_train.iloc[:,1],c=y_train)
ax.plot(X_train.iloc[:,0],(-w1*X_train.iloc[:,0]-w0)/w2)
ax.scatter(X_test.iloc[:,0],X_test.iloc[:,1],c=y_test)
ax.set(xlim=(2.9,7),xticks=[3,4,5,6,7],
ylim=(0.9,2.6),yticks=[1,2,2.6])
plt.show()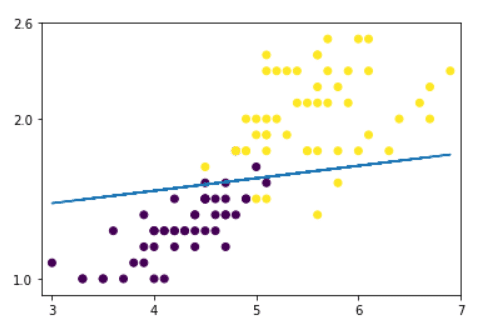
O Perceptron só consegue separar dados linearmente separáveis
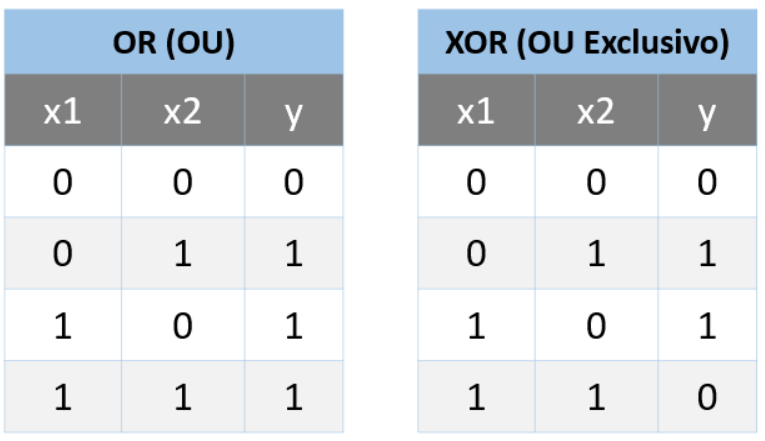
Este é o problema que prejudicou o Perceptron na década de 80, este foi um problema simples, mas se o Perceptron não conseguia resolver nem mesmo algo tão simples então não poderia ser considerado um bom algoritmo naquela época.
Após isso ele foi utilizado na forma de redes neurais e então conseguiu resolver este problema.
OR
O OR é uma condição lógica que vai dizer que se x1 e x2 é igual a 0, então o y é 0.
Se pelo menos um valor for 1, então o y vai valer 1
O XOR (OU Exclusivo)
Neste caso é preciso apenas 1 valor verdadeiro, se for verdadeiro e falso então o resultado é verdadeiro, se forem dois verdadeiros ou os dois falsos então o resultado é falso.
# Vamos considerar inicialmente os dados abaixo
Dados = pd.DataFrame({
‘x1’: [0,0,1,1]
,’X2’: [0,1,0,1]
,’Y’: [0,1,1,1]# Visualizando a base
dados
# E observando graficamente
fig, ax = plt.subplots()
ax.scatter(dados.x1,dados.x2,c=dados.y)
ax.set(xlim=[-0.1,1.1],xticks=[0,1],
ylim=[-0.1,1.1],yticks=[0,1])
plt.show()
Este é um caso que o Perceptron consegue resolver.
# Criando o classificador
clf = Perceptron(tol=1e-3, random_state=0,eta0=0.1)
# Selecionando X e y
X = dados[['x1','x2']]
y = dados.y
# Fazendo o fit com os dados
clf = clf.fit(X,y)
# Fazendo a previsão
y_pred = clf.predict(X)
y_pred
array([0, 1, 1, 1], dtype=int64)
# Avaliando o modelo
confusion_matrix(y,y_pred)
array([[1, 0]
[0, 3]], dtype=int64)# Verificando o coef_
clf.coef_
array([[0.2, 0.2]])
# Verificando o intercept_
clf.intercept_
array([-0.1])
# Podemos escrever w1, w2 e w0 como
w1 = round(clf.coef_[0][0],2)
w2 = round(clf.coef_[0][1],2)
w0 = clf.intercept_[0]
print(w1,w2,w0)
0.0 0.0 0.0
# Visualizando esse resultado graficamente
fig, ax = plt.subplots()
# Criando um array de x
x_perc = np.linspace(-0.1,1,100)
# Agora calculando o y
y_perc = (-w1*x_perc-w0)/w2
ax.scatter(dados.x1,dados.x2,c=dados.y)
ax.plot(x_perc,y_perc,'r')
ax.set(xlim=[-0.1,1.1],xticks=[0,1],
ylim=[-0.1,1.1],yticks=[0,1])
plt.show()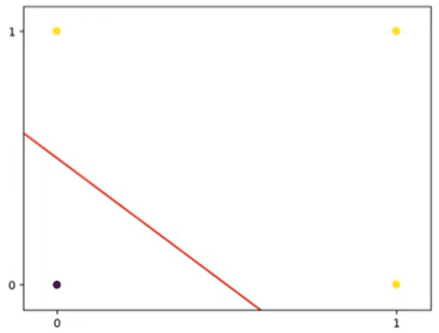
Vamos voltar e fazer para o caso do XOR
# Vamos considerar inicialmente os dados abaixo
Dados = pd.DataFrame({
‘x1’: [0,0,1,1]
,’X2’: [0,1,0,1]
,’Y’: [0,1,1,0]
# Visualizando a base de dados
# E observando graficamente
fig, ax = plt.subplots()
ax.scatter(dados.x1,dados.x2,c=dados.y)
ax.set(xlim=[-0.1,1.1],xticks=[0,1],
ylim=[-0.1,1.1],yticks=[0,1])
plt.show()
Observe que não é linearmente separável!
# Criando o classificador
clf = Perceptron(tol=1e-3, random_state=0,eta0=0.1)
# Selecionando X e y
X = dados[['x1','x2']]
y = dados.y
# Fazendo o fit com os dados
clf = clf.fit(X,y)
# Fazendo a previsão
y_pred = clf.predict(X)
y_pred
array([0, 0, 0, 0], dtype=int64)
# Avaliando o modelo
confusion_matrix(y,y_pred)
array([[2, 0]
[2, 0]], dtype=int64)
# Verificando o coef_
clf.coef_
array([[0., 0.]])
# Verificando o intercept_
clf.intercept_
array([0.])
# Podemos escrever w1, w2 e w0 como
w1 = round(clf.coef_[0][0],2)
w2 = round(clf.coef_[0][1],2)
w0 = clf.intercept_[0]
print(w1,w2,w0)
0.2 0.2 -0.1
# Visualizando esse resultado graficamente
fig, ax = plt.subplots()
# Criando um array de x
x_perc = np.linspace(-0.1,1,100)
# Agora calculando o y
y_perc = (-w1*x_perc-w0)/w2
ax.scatter(dados.x1,dados.x2,c=dados.y)
ax.plot(x_perc,y_perc,'r')
ax.set(xlim=[-0.1,1.1],xticks=[0,1],
ylim=[-0.1,1.1],yticks=[0,1])
plt.show()
Observe que ele não foi capaz de classificar:
C:\Users\Jean Luca\AppData\Local\Temp\ipykernel_8984\3847935731.py:8:RuntimeWarning: invalid value encountered in true_divide
y_perc = (-w1*x_perc-w0)/w2
Neste caso ele não conseguiu gerar nenhum resultado, apesar de conseguir separar bem casos lineares, o Perceptron não foi eficiente em um caso “simples” como o OU Exclusivo, colocando em xeque a sua funcionalidade durante um bom tempo
Até que o ganho do poder computacional e o aumento na quantidade de dados permitiram conectar vários Perceptrons em várias camadas e com essa quantidade maior de Perceptrons trabalhando juntos o resultado apareceu e o projeto foi retomado.
Nesta aula foi apresentado o Perceptron, o que é e para que é utilizado, também fizemos dois exemplos de casos reais que mostram o porquê do modelo ter ficado congelado tantos anos.
Vimos também o que mudou para que hoje com o ganho de poder computacional o Perceptron ter sido retomado e é o mais promissor nas áreas de inteligência artificial!
Eu fico por aqui! Até a próxima!
Para acessar outras publicações de Ciência de Dados, clique aqui!
Expert em conteúdos da Hashtag Treinamentos. Auxilia na criação de conteúdos de variados temas voltados para aqueles que acompanham nossos canais.